Six Shifts for Math Teachers Moving Online

Adam Lavallee is a math and economics teacher at The Episcopal Academy. He is also a GOA teacher and Learning Design Coach.

When I talk about online learning with mathematics teachers of core courses (Algebra 2, Precalculus, etc.) the most frequent question I get is: What is a model of a successful online learning space for my course? The truth is, there is not a one-size-fits-all solution: each school is different, each teacher is different, and each student is different. We must design our math courses by leaning into best online learning practices, which are not discipline-specific but rather a menu of pedagogical strategies.

Rather than simply show one model, which would only serve to create imitator courses and stifle innovation, I’ve developed a list of six shifts for teachers, with math teachers specifically in mind. I've gathered some examples from teachers who participated in GOA's Designing for Online Learning course and Design Bootcamp to help illustrate these ideas.

These shifts consider a transition from a traditional math classroom to an engaging online course with a robust community of learners that allows for student choice, timely feedback, content coverage, and student mastery. While I focus on math courses here, all teachers will find applications relevant to their own classes and curricula.

1. Content

Shift: Examine each component of your course content to determine which content is essential and whether students should master it, explore it, or be exposed to it. Then, choose to allot time (both teacher time and student time) as appropriate,. If the goal is for lasting understanding, spend more time. If the goal is mechanical fluency (i.e. factoring) then make that public, drill, revise, and revisit.

Mathematics curriculum is packed full of content. Because content is traditionally spiraled, teachers (and departments and schools) must be intentional about which content needs significant time for students to learn, understand, and master. Other content can be eliminated or limited to observation or exposure.

Consider this approach to Algebra 2, which could serve as a framework for discussing content with colleagues:

• The fantastic Larson Algebra 2 textbook contains four sections in chapter 3 devoted to matrices (and applying Cramer’s rule to solve systems). From my perspective, this is a piece of content that is non-essential. This method for solving a system of equations does not do matrices justice. Matrices can do so much and deserve a course of their own (see Linear Algebra). Thus, barely scratching the surface with a mechanical- or calculator- process does not do this content justice. I would eliminate this content from my course in order to focus on content students will need to master to move to precalculus.
• In the same course, a piece of content that I want students to observe, but not do (I don’t even have them take notes) is using completing the square to derive the quadratic equation. I will record this derivation in an EdPuzzle, ask students a few questions for accountability, and move on.
• Logarithms is a concept I want students to have exposure to and practice with, so that they can work for greater understanding in a subsequent course. I will not have a summative assessment, but will ask students to master a few fundamental concepts (i.e. logarithms are inverses of exponential functions, are used to convert between exponential and logarithmic form, and are used to solve exponential equations).
• A component that is essential to Algebra 2 is functions. After carving out space and time on the first three bullet points, I can ask students to spend more time mastering and reflecting on functions. I can try to assess for understanding in multiple applications, and most importantly, I can allot synchronous time to helping students work toward competency.

2. Content Delivery

Shift: Move content delivery to asynchronous, online, and on demand videos for students. Then, use synchronous time (in small groups if possible) to work through example problems, extending problems, and misconceptions. The key strategy is a structure where students know their objectives, and they have the ability to check for their own understanding along the way.

Example:

The following post from GOA’s Design Bootcamp by participant Emina Alibegović (Rowland Hall) gives a sense of possibilities within a math classroom:

“I think that delivery via video is one of the ways to present ideas that students can't necessarily discover on their own. If you choose to 'deliver' the material through video, the issue is that you don't know what the students gained from it, what questions they still have, and what they actually understand. Edpuzzle is a really good tool that allows you to:

• Ask questions of students during the video presentations.
• Provide notes you may want the students to have, or maybe remark on something that is important in the video that you want to emphasize.
• Allow them to ask a question of you and for you to respond."

Another tool for mathematics classroom is Geogebra. You can make experiences in which you embed activities and follow it up with questions such as the one I list below. You can have a conversation with your students. Here's an example.

3. Homework

Shift: Eliminate “homework,” and just call it learning. Students need practice. We need to incentivize authentic practice, so students take that work seriously. So, let’s take a page from our writing colleagues and treat homework as a first draft and “assess” the revision process. Then, there is no need to give students points just for completing their homework.

Example:

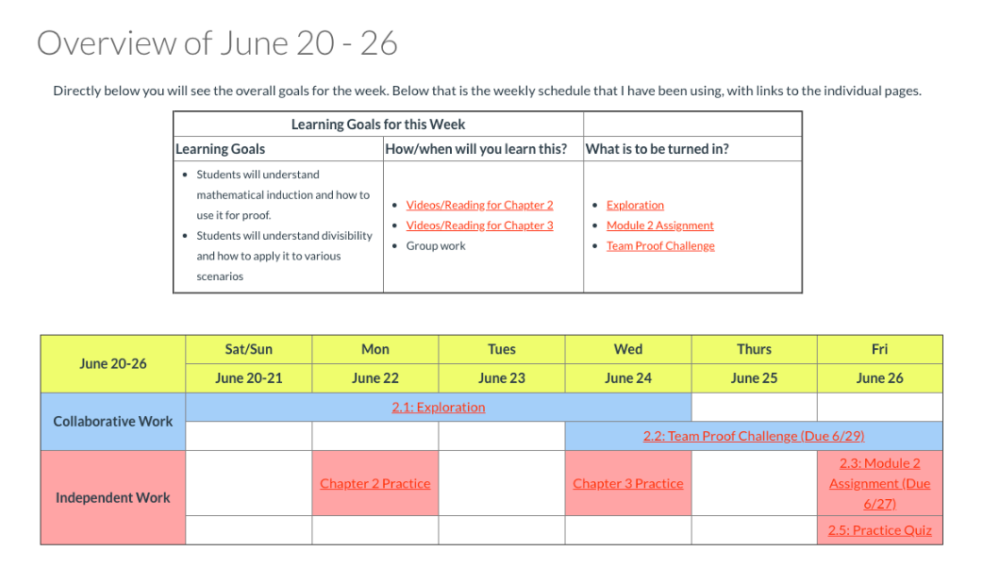
Student work does not have to be linear or in lock step. GOA teachers Jim Wysocki (Catlin Gabel School) and Andy Talmadge (Metairie Park Country Day School) share this flexible timeline here:

And while students complete work, problems can be grouped to clarify expectations for students. Consider how math teacher Avery Pickford reframes categorizing problems in this tweet:

Students could then submit the entire problem set to a public discussion board. Many discussion boards allow students to only see replies once they have submitted a response (for example, here’s how to do it in Canvas LMS). If the first “response” they see is a completed solution set, then they can check their own work and that can be the assignment that is graded. Assess students not on their first draft of homework or their final product, but on their revisions and reflections. Let them see the final solutions, then focus on, assess, and incentivize the revision process.

4. Feedback

Shift: Use automation to give instantaneous feedback to students. Broadcast feedback to address the whole class (this is an aspect that transfers particularly well from face-to-face to online). Allow students to submit work, then see the solution set (as in a discussion board with responses hidden until submitted). Require students to self-assess. Make the self-assessment an assignment and learning outcome of its own. Let students provide support for each other. They can become experts at a certain problem or type of problem and create tutorials both to grow and help others.

Example:

In the Design Bootcamp, Scott Britton (Woodstock School) created an EdPuzzle video with embedded questions. While this example is for a chemistry class, the opportunity for two-way asynchronous feedback is relevant to math teachers. First, as students progressed through the video, they answered questions and were able to have a sense of their understanding. Then, the teacher is able to see student responses both individually and in aggregate to gauge next steps. Students can then be grouped by accuracy, or a synchronous session could be designed to incorporate questions on which the class struggled. For an explanation of EdPuzzle, see this overview I made.

5. Interaction

Shift: On a video call, it’s much harder for a student to ask a question or lean to a classmate to make sure they are on the right track. It’s much harder for a teacher to “walk by” and connect with students doing individual practice. Teachers need to intentionally design for interaction in online formats and create structures that empower student voices in online and hybrid classrooms like those outlined in this GOA Relationships by Design Playlist.

Below are two contributions from math teachers.

Example 1:

Marianne van Brummelen (The Masters School) shared in a recent GOA Design Bootcamp a video loaded with practical examples of relationships, agency, and feedback. Most importantly, students are interacting with each other and interacting with math.

Example 2:

Rebecca Swanson (American Community School, Abu Dhabi), a participant in GOA’s Designing for Online Learning course, shared her approach:

"I assigned each student a focus problem once a week. Their job was to create a video explaining the problem as though we were in class and their partner didn't understand and I was unavailable to help. These were formative assessments, but if I heard something I didn't like, I was able to arrange a tutorial session with that student to clarify. The added benefit is that there were video explanations for loads of the practice problems, so students who were stuck had an additional resource for support. The first couple of weeks of doing this, I recorded my own example videos, too, just to give them a better idea of what I was looking for. They were a big hit."

6. Assessment

The online environment supports a diverse set of assessment strategies. I prefer a three-fold approach to summative assessment in an online math classroom.

Example:

Automate some assessment. Thoughtful multiple choice problems like the following assess student conceptual understanding. Create 20 and have an assessment that randomly chooses 10 for students to complete in 15 minutes.

Use student oral exams to have students walk through a solution to a multi-stepped problem. These can last 5-10 minutes and teachers can ask questions and provide support when needed. This allows students to describe their thinking and conceptual understanding.

Use Capstone Projects. Let students demonstrate their understanding with choice. Each unit can conclude with students exploring an authentic application of their choosing. Topics can include regression, parabolic motion, and optimization.

Shifting to online teaching can feel overwhelming. It's important to consider these shifts carefully and focus on the work most relevant to your students and your context. Then, incorporate more and more shifts over time. As with any new skill, mastery of online teaching requires practice, time, and patience.

GOA has several opportunities for educators to develop their online teaching and design skills. Explore our educator courses and programs. For more articles and resources on using online spaces in teaching and leadership, visit our COVID-19 hub.